Simplifying Algebra

...

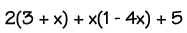
source



Simplifying Equations

To find a solution for an equation, we can use the basic rules of simplifying equations. These are as follows:
1) You may evaluate any parentheses, exponents, multiplications, divisions, additions, and subtractions in the usual order of operations. When evaluating expressions, be careful to use the associative and distributive properties properly.

2) You may combine like terms. This means adding or subtracting variables of the same kind. The expression 2x + 4x simplifies to 6x. The expression 13 - 7 + 3 simplifies to 9.

3) You may add any value to both sides of the equation.

4) You may subtract any value from both sides of the equation. This is best done by adding a negative value to each side of the equation.

5) You may multiply both sides of the equation by any number except 0.

6) You may divide both sides of the equation by any number except 0.

Hint: Since subtracting any number is the same as adding its negative, it can be helpful to replace subtractions with additions of a negative number.

Example:

This problem illustrates grouping like terms and dealing with subtraction in an equation.

Solve x - 12 + 20 = 37.

Replacing the -12 with a +(-12), we get

x + (-12) + 20 = 37.

Since addition is associative, the two like terms (the integers) may be combined.

(12) + 20 = 8

The left side of the equation becomes

x + 8 = 37.

Now we may subtract 8 from each side of the equation, (we will actually add a -8 to each side).

x + 8 + (-8) = 37 + (-8)

x + 0 = 29

x = 29

We can check this solution in the original equation:

29 - 12 + 20 = 37x + 0 = 29

17 + 20 = 37

37 = 37 so our solution is correct.

Example:

This problem illustrates the proper use of the distributive property.

Solve 2 × (x + 1 + 4) = 20.

Grouping like terms in the parentheses, the left side of the equation becomes

2 × (x + 1 + 4) ==> 2 × (x + 5).

Using the distributive property,

2 × (x + 5) ==> 2 × x + 2 × 5.

Carrying out multiplications,

2 × x + 2 × 5 ==> to 2x + 10.

The equation now becomes

2x + 10 = 20.

Subtracting a 10 (adding a -10) to each side gives us

2x + 10 + (-10) = 20 + (-10) ==>

2x + (10 + (-10)) = 20 - 10 ==>

2x + 0 = 10 ==>

2x = 10.

Since the x is multiplied by 2, we divide both sides by 2 to solve for x:

2x = 10 ==>

2x ÷ 2 = 10 ÷ 2 ==>

(2x)/2 = 5 ==>

x = 5.

We can check this solution in the original equation:

2 × (5 + 1 + 4) = 20 ==>

2 × 10 = 20 ==>

20 = 20 so our solution is correct.